기존의 Convolutional Neural Network(이하 CNN)의 문제점은 네트워크의 깊이가 깊어질수록 연산량이 늘어나 컴퓨팅파워가 부족했던 2010년 전후는 Layer를 깊이 쌓지 못하였다. 또한 Vanishing Gradient문제도 이점에서 한몫 하였다.
그래서 AlexNet은 8층, VGC는 19층, GooleNet은 22층에 불과했으며, 많은 연구들이 20층 내외의 층에서 실험을 진행했다. 그래서인지 사람만큼의 퍼포먼스를 보여주지는 못하였다.
2015년이 되어 혜성처럼 등장한 모델이 있었으니 바로 ResNet이다.
Concept
ResNet은 Residual Network의 약자로 잔차 의 개념을 도입한 방법이다. 이를 이해하기 위해서는 우선 Block의 개념과 Identity Mapping이라는 것을 알아야 한다.
1. Block
Block은 layer의 묶음 이다. 위 그림에서와 같이 Resnet에서는 2개의 Conv Layer를 하나의 Block으로 묶는것이다. 이러한 Block을 Residual의 이름을 따서 이를 Residual Block이라고 부르기도 한다.
이런 Residual Block을 여러개를 쌓아간것이 ResNet의 구조인것이다. 하지만 여기서 문제가 발생한다. Layer를 쌓을수록 늘어다는 Parameter의 갯수가 문제이다.

위 그림의 예시인 ResNet-34는 Conv Layer가 34개가 있으며 16개의 Block으로 감싸져있다.
첫번째 Block의 Parameter 갯수를 살펴보면 3x3x64의 Convolution Layer가 2개가 있으므로 1.152K가 된다. 전체 Parameter의 갯수를 세어보면 21,282M이다.
이제 Layer가 더욱 깊어지면 Parameter의 수는 더이상 컴퓨터가 감당할 수 없을 지경일지 모른다. 그래서 저자는 Bottleneck Block이라는것을 제안한다.
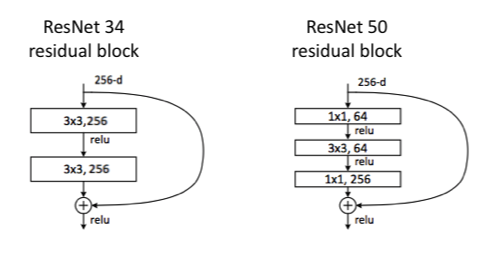
ResNet-34와 ResNet-50에서의 Block구조이다. ResNet-34에서의 Block은 2개의 Conv Layer가 들어가있으며 Parameter의 수는 3x3x256x256+3x3x256x256 = 39.3216M 이 된다.
반면 ResNet-50에서의 Block은 3개의 Conv Layer가 들어가 있으며 Parameter의 수는 6.9632M 이 된다. Parameter의 수가 무려 6배정도 감소되었음을 알 수 있다.
Conv Layer를 자세히 보면 ResNet-34와는 다르게 3x3 Conv Layer의 앞뒤로 1x1 Conv Layer가 붙어있는데, 1x1 Conv Layer가 채널의 수를 조절하면서 차원을 줄였다 늘리는 역할을 하는 것이다.
이 부분이 마치 병목과 같다 하여 Bottleneck Block 라고 불리게 되었다.
2. Identity Mapping(Shortcut, Skip Connection)
위 그림을 자세히 보면 왠 + 기호가 있는것을 볼 수 있다. 이 부분이 바로 Identity Mapping이라고 하는 부분이다.
Identity Mapping이란 입력으로 들어간 값 $x$가 어떠한 함수를 통과하더라도 다시 $x$가 나와야 한다. 고등학교때 배운 항등함수 개념이다.
여기를 수식적으로 풀어보면 상당히 어려운데, 코드를 보면 직관적으로 이해할 수 있다.
class Bottleneck(nn.Module):
### torchvision의 resnet 코드입니다.
...
...
def forward(self, x):
identity = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
if self.downsample is not None:
identity = self.downsample(x)
out += identity
out = self.relu(out)
return outforward에서 가장 첫 Line에 x를 identity라는 변수에 따로 저장한다. 그리고 x는 Conv Layer를 통과해 내려가다가 맨 마지막에 bn3까지 통과한 FeatureMap인 out이라는 변수에 identity를 더한다.
예를들어 x가 (28, 28, 64)인 FeatureMap이라고 해보자.
identity의 형상은 그대로 (28, 28, 64)이고, Conv Layer을 타고 마지막 bn3까지 통과한 FeatureMap의 형상 또한 (28, 28, 64) 그대로이다. 같은 형상의 Matric을 더하는 것이므로 Element-wise sum이 되어 최종 FeatureMap의 형상은 그대로 (28, 28, 64)가 된다.
3. DownSample
위 그림과 코드를 보면 또하나의 궁금한점이 발생한다. 도대체 downsample은 무엇인가? 위 그림에서 실선으로 되어있는게 Identity Mapping인건 알겠는데 점선은 뭐지??
바로 FeatureMap의 형상이 축소되는 지점에서 일어나는 이벤트이다. 즉, pooling이 되는 부분이다.
맨위 그림의 보라색 영역을 살펴보면, 첫번째 Block에서 FeatureMap의 형상이 (28, 28, 64) 였다면 세번째 Block의 마지막 Conv Layer를 통과하고 Identity Mapping까지 완료된 FeatureMap의 형상도 (28, 28, 64)이다.
녹색 영역의 시작지점에서는 채널의 수가 128로 늘어났고, /2 라는 것으로보아 첫번째 Block에서 Conv Lyaer의 stride가 2로 늘어나 (14, 14, 128)로 바뀐다는것을 알 수 있다.
코드를 살펴보면, Identity의 형상은 보라색 영역의 FeatureMap 형상인 (28, 28, 64)이다.
즉, 여기에서 형상을 맞춰주지 않으면 Identity Mapping을 할 수 없게된다. 그래서 이 Identity에 대하여 downsample을 해주는것이 필요하다.
맞춰주는 방법은 매우 간단하다. stride 2를 가진 1x1 Conv Layer를 하나 연결해주기만 하면된다.
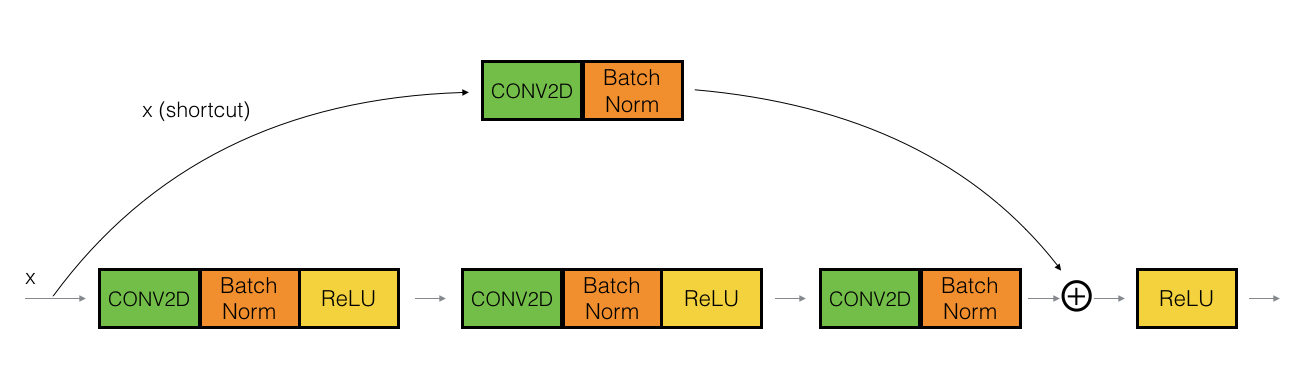
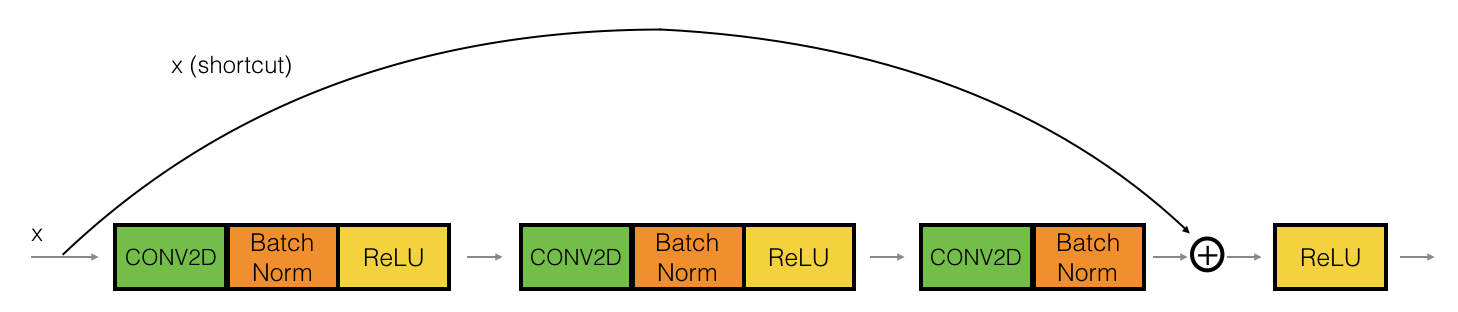
이렇게 DownSample을 하여 연결되는 방법을 Projection_shortcut이라고하고, 해당 Block의 영역을 특별히 Convolution Block이라고 부른다. 일반적인 shortcut 형태는 Identity Block이라고 한다.
4. Pre-Activation
ResNet 모델에서는 가중치 초기화 방법으로 He, Xaiver와 같이 잘 알려진 초기화 방법을 사용하지 않았다.
다만 Conv Layer의 뒤에 Batch Normalization(이하 BN)을 취해주는 방법을 사용했다. 그리고 BN과 Activation Layer의 순서를 다양한 방법으로 변경하면서 퍼포먼스를 실험해 보았다.
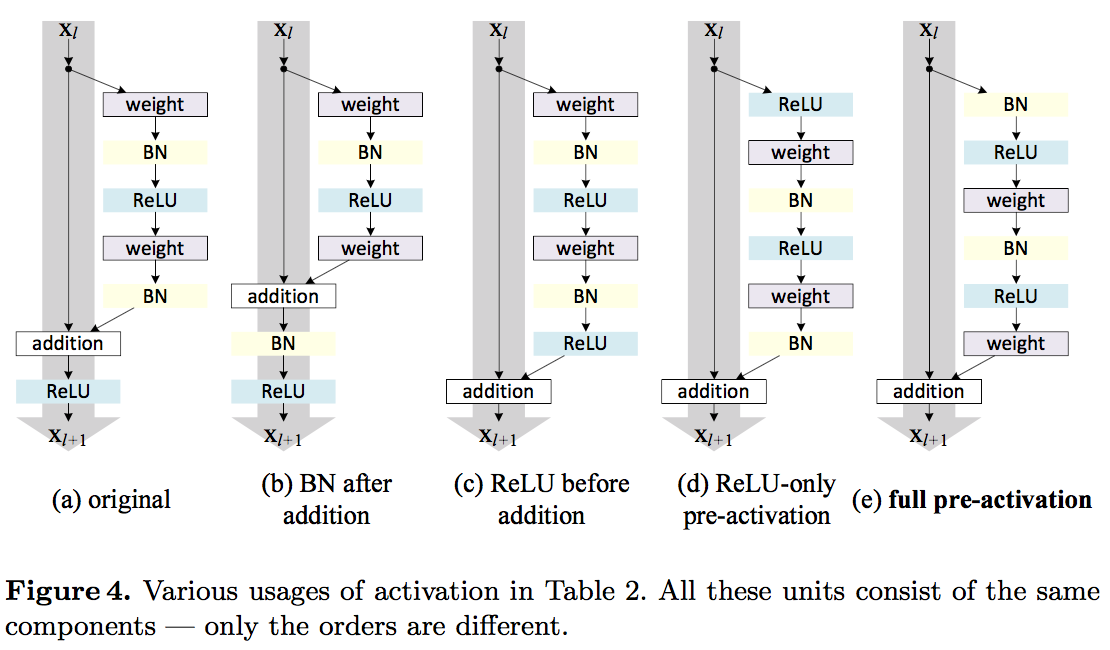

기존의 방법인 (a)를 보다 ReLU앞에서 BN을 해준 (e) 방법이 더 뛰어난 퍼포먼스를 보인다. 이에대하여 저자는 두가지 이유로 인해 더 좋은 퍼포먼스를 보인다고 말한다.
- Pre_activation은 역전파를 할 때 Activation 함수인 ReLU에서 truncated될 여지가 없다.
- Batch_normalization이 ReLu이전에 있기 때문에 입력으로 들어온 데이터정규화(regularization) 측면에서 개선되었다.
ResNet의 이러한 아이디어는 이후에 나오는 논문에서 상당한 영향을 미쳤고 특히 Skip Connection은 현재까지도 사용되고있는 핵심 테크닉이 되었다.
또한 Object Detection, Segmentation에서 Backbone으로도 자주 사용되고 있으며 현재기준으로 인용수 56,517회 일정도로 유명하다. 딥러닝을 하는 사람이라면 모르고 넘어갈 수 없는 모델인만큼 꼼꼼히 익혀두자.
Appendix
Identity Mapping
위에서 간단히 설명했던 개념을 좀더 구체적으로 알아 보도록 한다.
Identity Mapping이란 Identity Function $h(x)=x$를 만족하도록 하는것임은 이제 알았다.

위 그림은 일반적인 CNN의 구조이다. 입력으로 들어온 $x$가 weight layer(Conv layer와 동치)를 지나가고 활성함수 relu를 통과하는 형태이다. 우리는 이렇게 통과하고 나온 최종적인 형태인 $H(x)$를 최적화 하는것을 목표로 삼는다.

위 그림이 바로 ResNet의 Identity Mapping구조이다. 입력으로 들어온 $x$를 weight layer을 통해 아래로 흘러 내려온 부분을 $F(x)$라 한다면 $H(x)=F(x) + h(x)$가 되고, Identity Function에 의해 $h(x)=x$가 되어 $H(x)=F(x) + x$가 된다. 이렇게 나온 출력 $H(x)$는 다음 레이어의 인풋으로 들어간다.
$$
y_{l} = h(x_{l}) + F(x_{l},W_{l}) = x_{l} + F(x_{l},W_{l})\
f(y_{l}) = x_{l+1}
$$
아래첨자 $l$은 Block 단위(Unit)이다. $h(x)$와 weight layer을 통해 내려온 $F(x)$가 더해져 출력 $y$가 되고 이는 Relu라는 activation function을 $f$를 통과해 다음레이어의 인풋이 된다.
하지만 저자는 이를 진정한 의미의 Identity Mapping이라고 생각하지 않았다. ResNet의 후속논문인 Identity Mapping in Residual Networks에서는 이러한 점을 개선한 부분이 등장한다.
바로 activation function 대신 Identity function을 취해주는것이다. 바로 함수 $H$를 다시 Identity Function이라고 생각한 것.
$$
x_{l+1} = h(y_{l}) = h(h(x_{l})) + F(x_{l},W_{l}) = x_{l} + F(x_{l},W_{l})
$$
조금 더 직관적으로 알아보기 위해 $l+2$번째까지 적어보면,
$$
x_{l+2} = h(y_{l+1}) = x_{l+1} + F(x_{l+1},W_{l+1})=x_{l} + F(x_{l},W_{l}) + F(x_{l+1},W_{l+1})
$$
이제 이를 하나의 식으로 작성할 수 있다.
$$
x_{L} = x_{l} + \sum_{i=l}^{L-1}F(x_{i},W_{i})
$$
어떠한 $L$번째의 Block의 출력은 초기의 입력받는 층($l$)과 그 이전까지 연결된 층의 합(SUM)으로 이루어져 있다는것이다.
이것은 연산 복잡도에 엄청난 영향을 미친다. 역전파를 진행할때 곱에대한 편미분보다 합에 대한 편미분이 훨씬 간단하기 때문. 상세하게 알아보기 위해 위 식을 $x$에 대해 편미분을 진행해 보자.
$$
\frac{\partial \varepsilon}{\partial x_{l}} = \frac{\partial \varepsilon}{\partial x_{L}}\frac{\partial x_{L}}{\partial x_{l}} = \frac{\partial \varepsilon}{\partial x_{L}}\left(1+\frac{\partial}{\partial x_{L}}\sum_{i=l}^{L-1}F(x_{i},W_{i})\right)
$$
$x_{l}$을 Loss Function($\varepsilon$)에 대하여 미분하였을때 $\frac{\partial \varepsilon}{\partial x_{L}}$와 $\frac{\partial x_{L}}{\partial x_{l}}$의 곱으로 표현된다.
앞쪽의 $\frac{\partial \varepsilon}{\partial x_{L}}$ L번째 Block단위의 정보를 뜻하고 이것은 $l$번째 Layer에 바로 전파된다.
뒷쪽의 $1+\frac{\partial}{\partial x_{L}}\sum_{i=l}^{L-1}F(x_{i},W_{i})$부분은 Loss Function이 있는 Layer에서 부터 $l$번째 Weight Layer까지의 편미분 합이 된다.
따라서 연산량도 줄어들 뿐만 아니라 Gredient가 사라지는 Vanishing 문제도 없어지게 되는것이다.(가중치 초기화 방법인 Xaiver나 He를 생각해보면, 초기화된 가중치를 모두 더했을때 -1이 나올 확률은 0에 수렴한다)
다시 위쪽의 $H(x)=F(x) + x$식을 보자. 진정한 의미의 Identity Mapping은 $H(x)=F(x) + x = x$가 된다. Identity의 가정이 성립되기 위해서는 $F(x)$가 0이 되어야 한다.
$x$를 좌변으로 이항하면 $F(x)=H(x)-x$가 되고 이것은 마치 잔차처럼 보이게된다.(마치 선형회귀모형에서 많이 보던 $y=X\beta + \epsilon$의 모습) 그래서 이 알고리즘이 Residual(잔차) Network가 된것이다.





최근댓글